Heterogeneous multi-scale architected Structures with topological control of their heterogeneity
Topological control of microstructures for advanced material engineering.
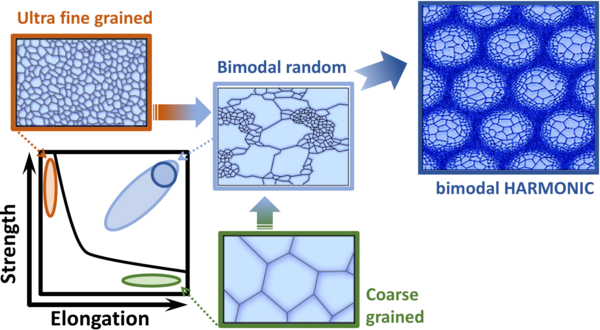
Natural materials typically demonstrate winning combination of properties, which comes from heterogeneous 'design' of their structure. Therefore, design and fabrication of artificial heterogeneous structures with precise control of their architecture across multiple scales has been emerging recently. This allows achieving simultaneous improvements in several, often disparate, properties, thus shifting materials to a more favourable property space.
Present project has primary objective to
- reveal the fundamental mechanisms of structural performance in new heterogeneous materials with topology-driven hierarchical structure designs, and
- develop fundamentals for their manufacturing.
This will become possible through unique in-house techniques for 'harmonic structured' materials fabrication as well as advanced characterisation facilities, including Neutron and X-ray sources and laboratory-scale electron microscopy, fatigue, other mechanical testing, along with extensive (inter)national collaborations. The experimental investigations will be guided by multi-scale simulations.
As a result of this project, the performance of such materials should reach horizons of functionality beyond the reach of existing material design concepts. These results will have a major impact spanning from enhanced understanding of novel material designs to the development of advanced low-footprint technologies to opening new horizons in sustainable life management.
Download MathLAB code
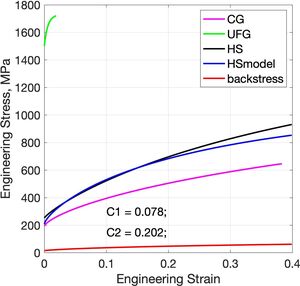
For the calculation of backstress and the fraction of plastically deforming UFG phase in harmonic-structure materials.
This is an open-source code for free use. it was developed as one of the results of a research project "Topological control of microstructures for advanced material engineering" Funded by Vetenskapsrådet, project # 2016-03811.
If you will publish the results of calculations using this code, please
- acknowledge the use of this code, and
- cite the following article where respective mathematical model was developed:
D.Orlov, R.Kulagin, Y.Beygelzimer, Strain partitioning and back-stress evaluation in harmonic-structure materials, Materials Letters (2020) 275, 128126; DOI: 10.1016/j.matlet.2020.128126
If you have any questions, comments, suggestions or requests, feel free to contact Dmytro Orlov (dmytro.orlov@material.lth.se).